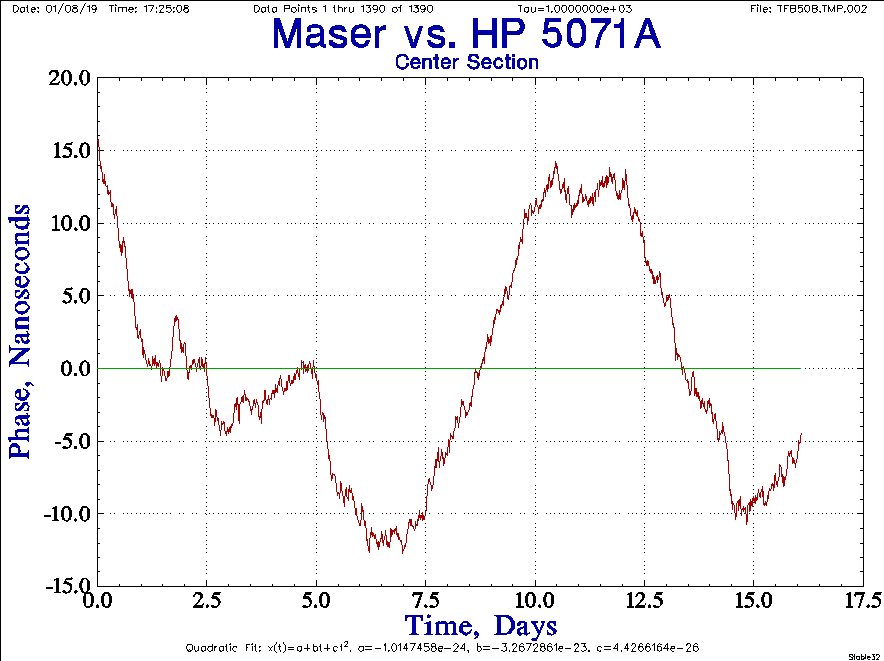
Maser Analysis: Long Term Performance
This page reports the results of long term (1.81 million seconds, or just under 21 days) measurement of the Morehead VLG-10-1 P2 maser made in late 2018.
This plot shows the ADEV (Allan Deviation) of the six measurements made during that period:
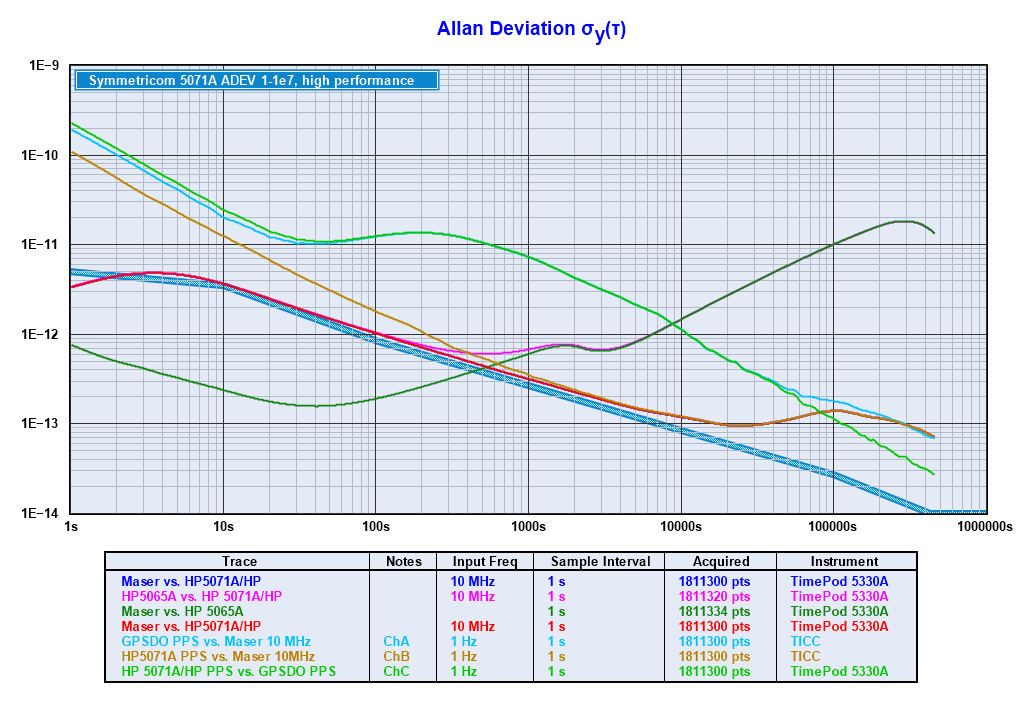
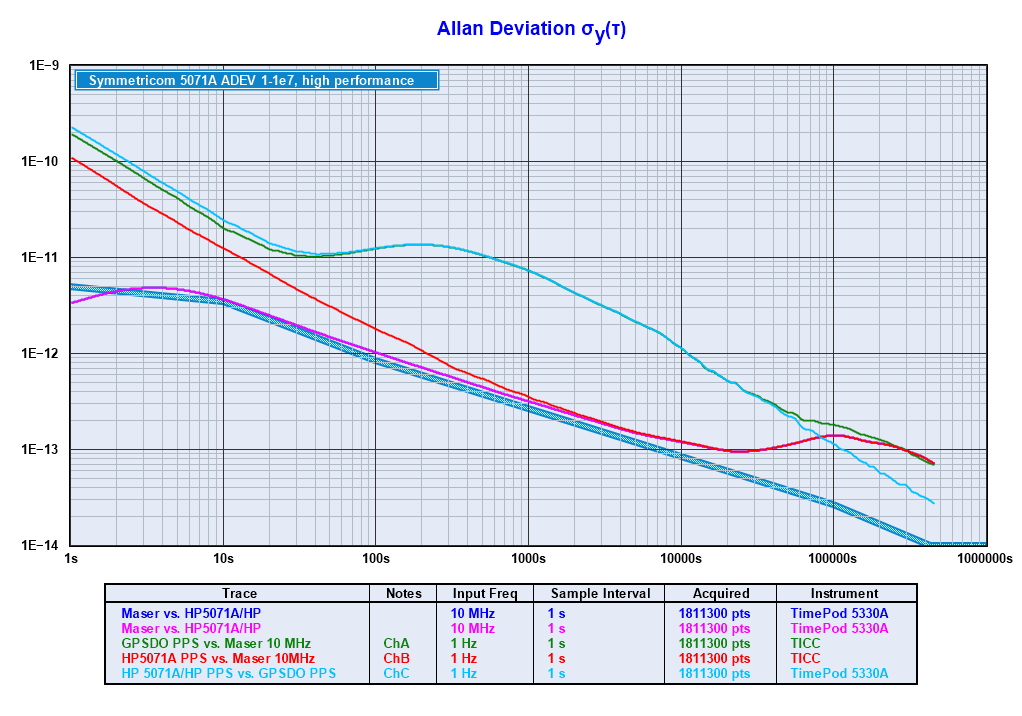
It's fairly obvious that the HP 5065A is not performing nearly as well as the other instruments, and it turns out that it was not functioning properly. The plot below is the same data, but without the 5065A trace. While the 5065A's performance makes it unusable for long-term stability measurements, it did have two periods where it performed well. Those are discussed on the Short Term Performance page
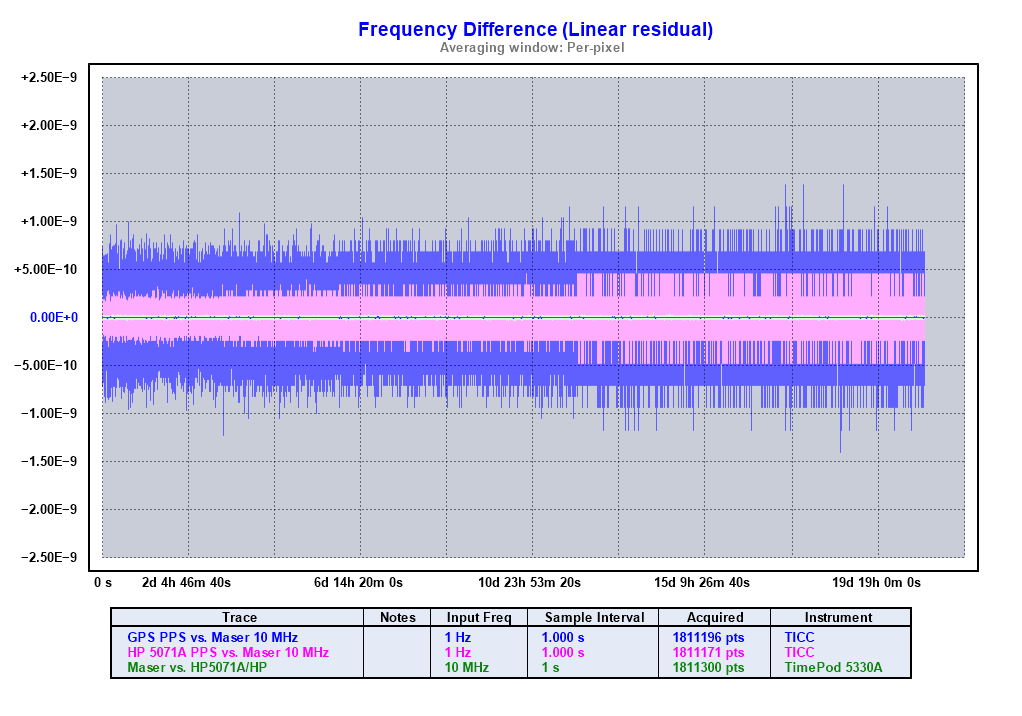
And this shows the frequency differences between the instruments (except the 5065A) over the course of the measurement:
These plots show the results taken at a 1 second rate, and we can learn some interesting and important things from them:
- The TICC's measurements are limited at short tau by its resolution and jitter of 60 to 80 picoseconds, which provides a measured ADEV floor of less than 8 x10-11 at one second, decreasing by an order of magnitude per decade: about 8x10-12 at 10 seconds, 8x10-13 at 100 seconds, and so on. At tau greater than about 1000 seconds, the TICC's resolution is sufficient to show the GPSDO and 5071A performance.
- The GPSDO plot shows an ADEV hump in the 100 to 1000 second region. This is characteristic of GPS disciplined oscillators, where the stability of the quartz crystal dominates at short tau, with GPS governing long term stability. The hump shows the area where the crossover occurs between the two regimes. A PPS derived solely from GPS would be much noiser at short tau, so this plot shows that this is a GPS disciplined oscillator and not raw GPS.
- But a GPSDO would usually be expected to have an ADEV in the 1 to several hundred second range of better than 1x10-11, quieter than the TICC. It shouldn't be much worse than the 5071A at these tau. The plot shows, though, that the GPSDO is better than the TICC only out to about 20 seconds -- far from the expected performance. The relative "fuzz" on the frequency chart makes it clear that the GPSDO is much noisier than any of the other sources at short tau. I don't know just what the hardware was that generated the GPSDO signal, but I suspect it's a unit designed more for telecom timing, than frequency generation, purposes.
- The TimePod resolution does not limit the measuremenit resolution at any tau. The maser vs. 5071A curve reported by the TimePod shows the performance of the cesium standard out to around 20K seconds, after which the drift of the maser causes the flattening and increase of the ADEV curve. The hump between 1 and 10 seconds is characteristic of cesium standards; it is the region where the quartz oscillator that acts as a "flywheel" transitions to the stability of the cesium beam. (The 5071A ADEV is specified as less than 8.5x10-14 at 10K seconds and less than 2.7x10-14 at 100K seconds, but only in the mid to low 12's below 10 seconds.)
- The step-like increase in the fuzz at about 1 million seconds seems like an artifact from the TICC counter. I need to investigate this.
The frequency chart shows how the visual noise created by showing nearly two million samples at a one second rate makes it really hard to see the details of longer term performance. For this reason, I'll use data averaged to 1000 or even 10,000 seconds for most of the subsequent frequency and phase plots on this page.
Frequency Traceability
Unless otherwise noted, the data set used on this page is a comparison of the maser to an HP 5071A Primary Frequency Standard. With its "high performance" option, it is specified to be within 5x1013 of the SI definition of the Hertz. It is considered a "primary" standard because its output is derived from the atomic transition that defines the SI Hertz; if the standard is operating properly, the 5071A's frequency will be within the stated error range of the atomic Hertz.
But it's good to verify this performance. The GPS navigation system relies on precise timing for its operation, and the "GPS time" used by the satellites is normally within 5 nanoseconds of US Naval time, known as UTC(USNO). The United States standards for frequency, time interval, and time- of-day are maintained by NIST; the timescale generated there is known as "UTC(NIST)". NIST and USNO make regular comparisons of UTC(NIST) vs. UTC(USNO). The differences between GPS time and UTC(USNO), and between UTC(USNO) are published on the web. Using this information, GPS time and time interval can be traced back to the official US standards. The GPS clock is normally within a handful of nanoseconds of UTC(NIST).
Commercial GPS receivers specified for timing use provide GPS time with second-to-second jitter as low as 10 to 15 ns RMS and an overall accuracy of 100 nanoseconds or better. Ten nanoseconds of jitter means a frequency stability at one second of 1x10-8. As the averaging interval increases, the stability improves on a decade-per-decade basis (slope of -1). That means that averaging of 100K seconds brings the GPS PPS stability to around 1x10-13.
A GPS-based PPS signal was available at the measurement location. Based on its observed performance, this signal is from a GPS disciplined oscillator ("GPSDO") of unknown brand and model number.
Along with the maser vs. 5071A comparison, a simultaneous measurement was made of the 5071A PPS vs GPS PPS. The two plots below show the results of that measurement.
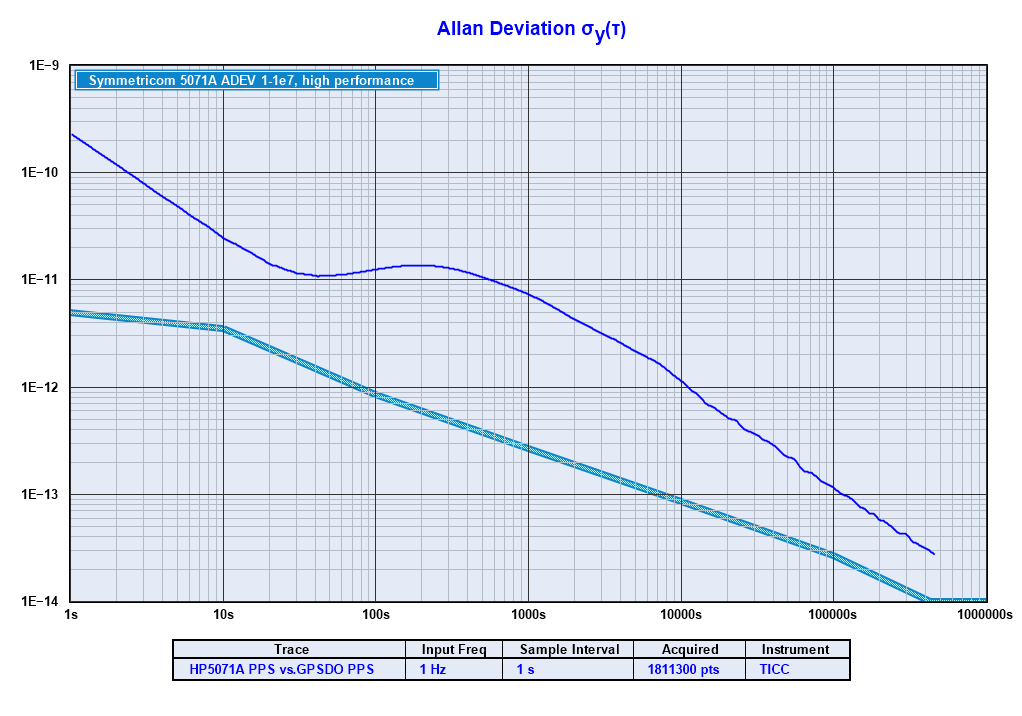
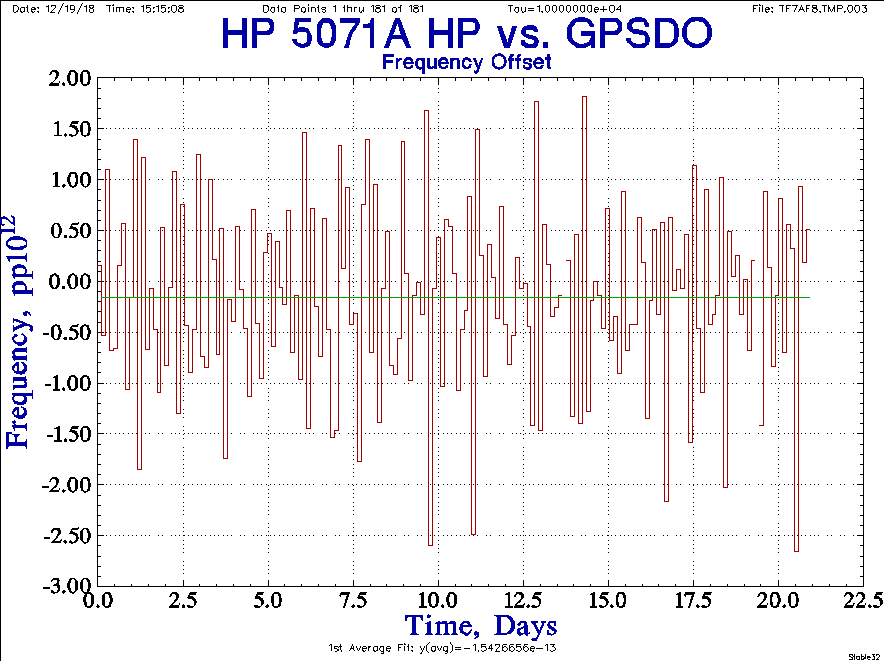
The second plot was made using the very excellent Stable32 software written by Bill Riley, who has graciously turned the code over to a free license. Stable32 has more extensive capabilities than TimeLab and in particular makes it easy to determine frequency offset over long measurements.
These plots show that the cesium and GPS performance have the expected -1 (decade per decade) slope with longer tau, and that the frequencies of the two are within 1.5x10-13 of each other, indicating that the 5071A's frequency is well within its specification. Subsequent tests confirm this frequency offset.
Maser Frequency Accuracy and Stability
Let's look at the maser's frequency compared to the 5071A, with 1000 second averaging. The first plot below is a graph of the maser's absolute frequency offset compared to the HP 5071A. The second plot moves the data to the center and expands the scale, but doesn't show the absolute offset.
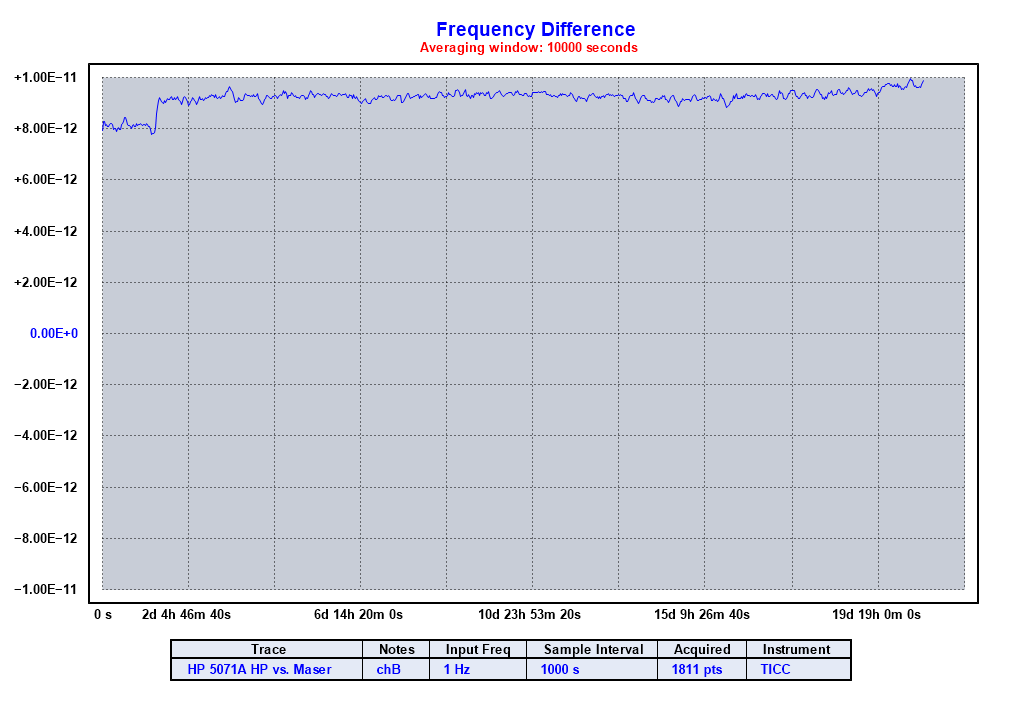
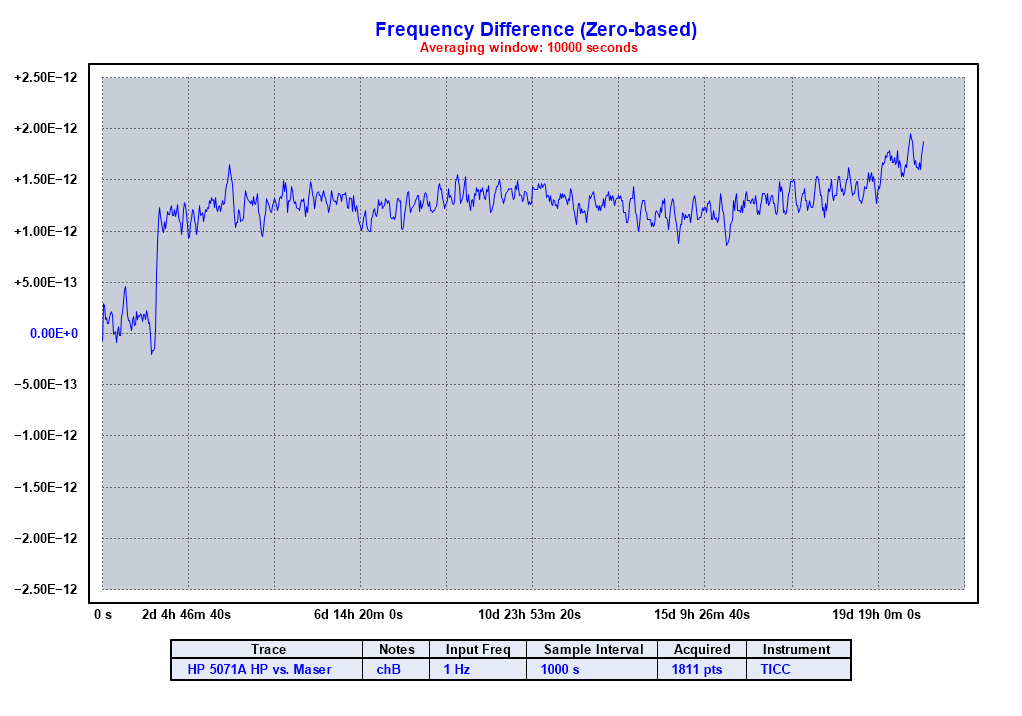
Notice that these plots show a couple of anomalies in the data. The first is a step frequency change that occurs near the beginning of the measurement. The second is a frequency drift that develops around 16 days in. They will be discussed below.
Frequency Offset
One important characteristice we want to learn about the maser is its absolute frequency, which should be 10 MHz precisely.
The first plot above shows that the absolute frequency difference between the maser and the 5071A is about 1x10-11. We know from above that the 5071A is within a couple of parts in 1013 of GPS, so we can take it as "accurate" for this purpose.
The two anomalies are on the order of one or two parts in 10-12 so are not large enough to make much impact on the average frequency over the full run.
Anomolies
These plots show the impact to the Allan Deviation if we trim the first anomaly, the second, and both:
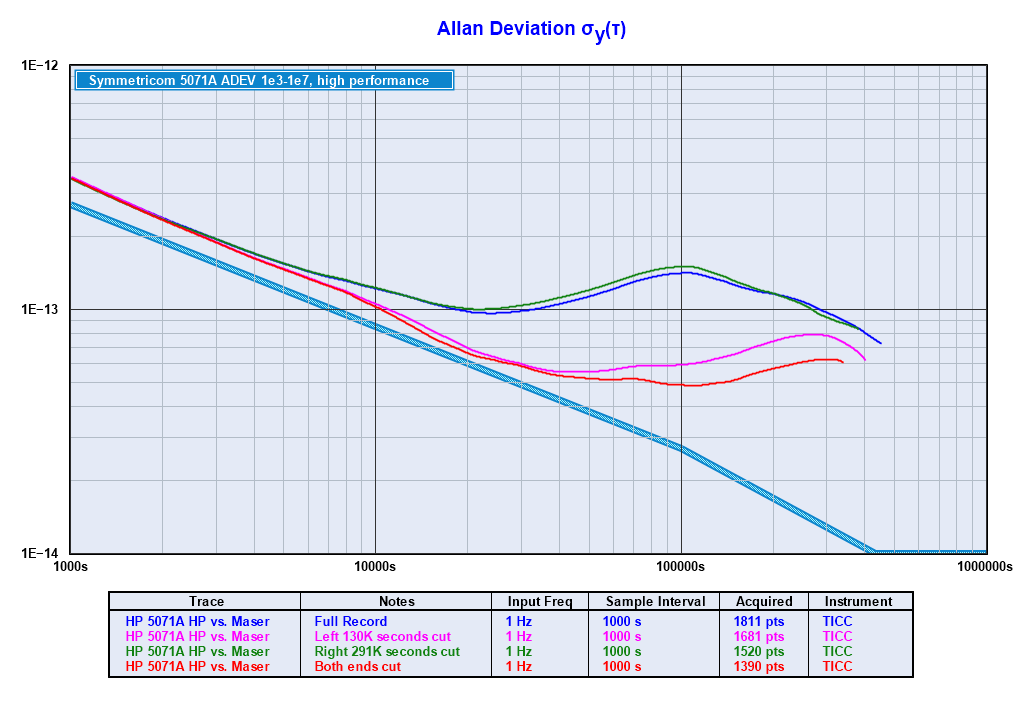
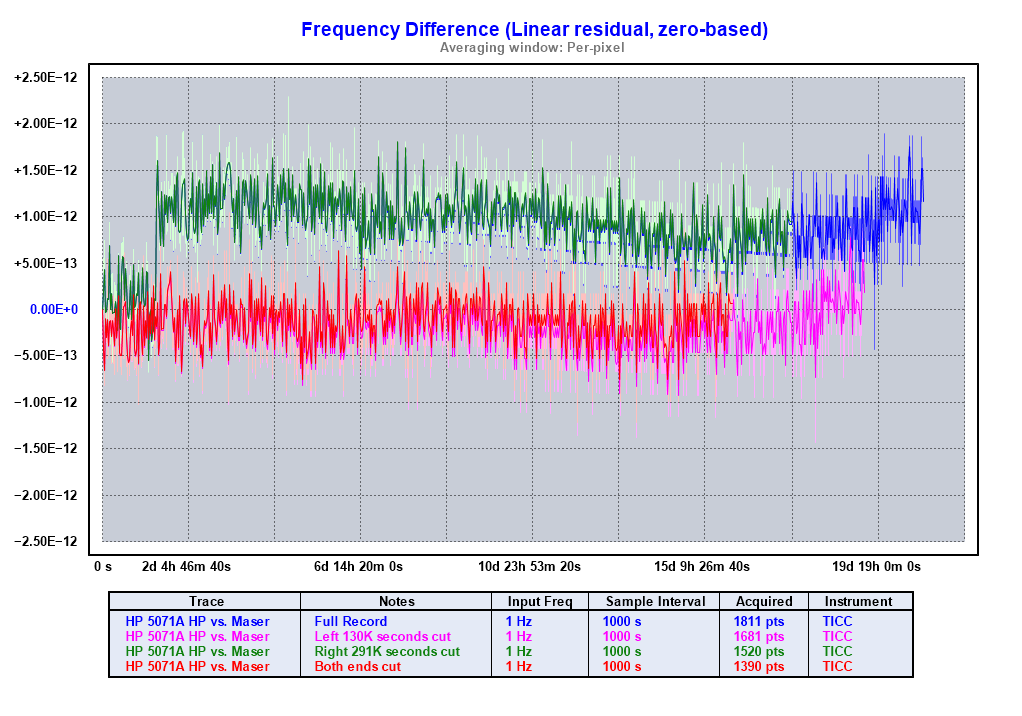
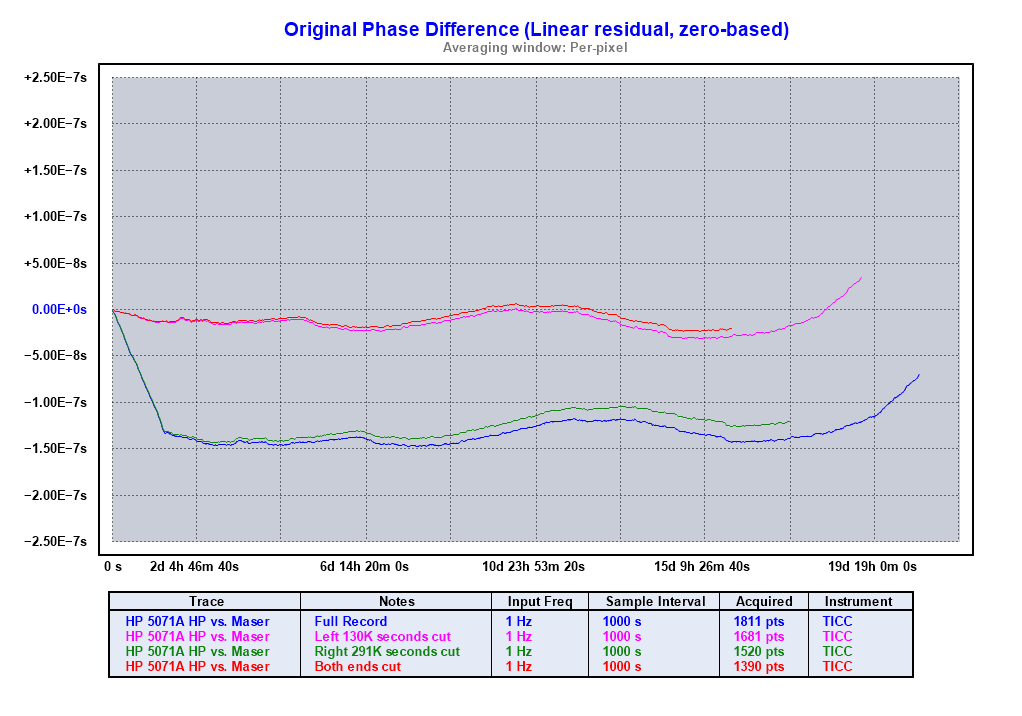
Frequency Step
Note the frequency jump that occurs at about 118500 seconds into the run. Here's a zoomed view of that time period with tau=1000 seconds:
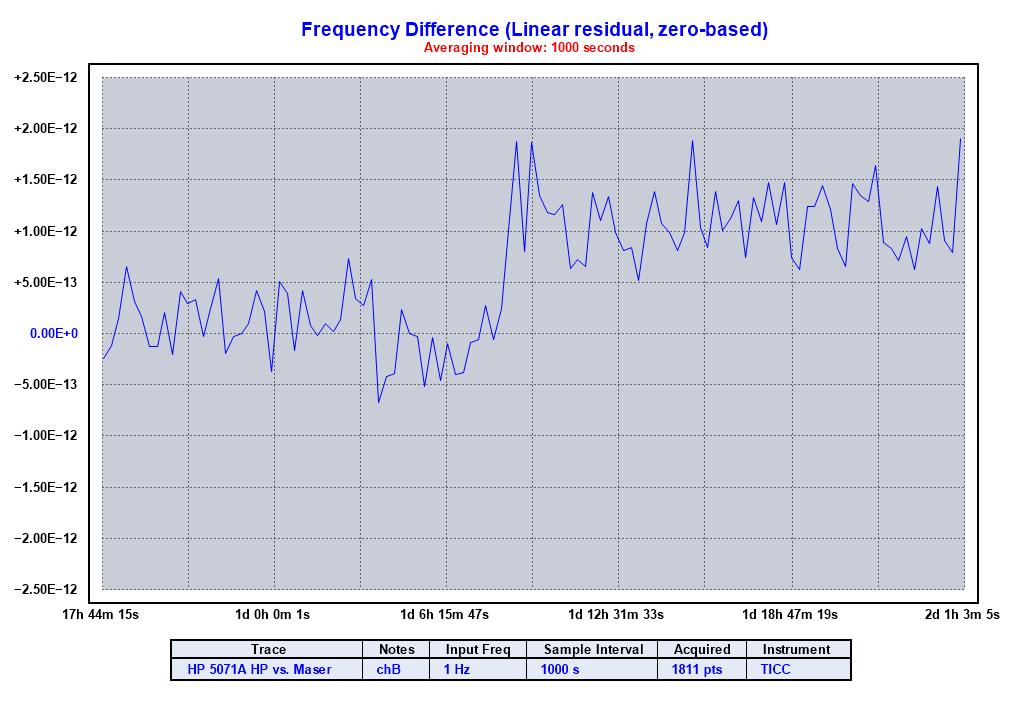
While the HP 5065A rubidium standard wasn't performing well, it was stable during this period, and its lower noise lets us see more clearly the speed of the frequency shift:
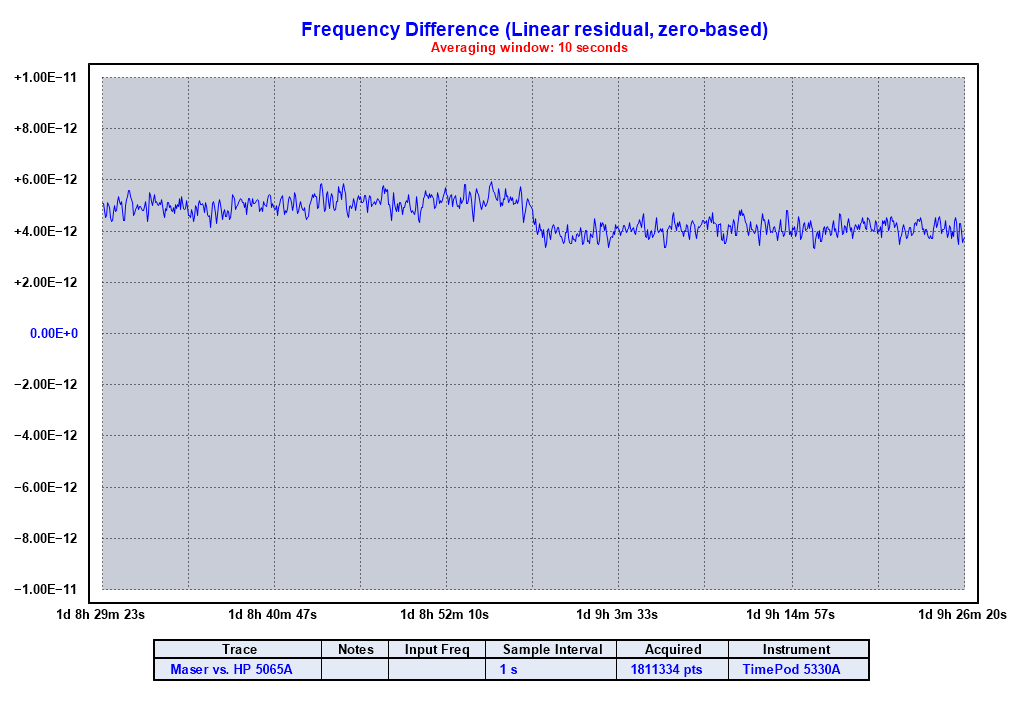
It appears that the frequency made a step change that occurred over about two minutes. The reason for this change is unknown. (Note that the direction of the change is reversed from the prior plots. That's because the two measurement instruments had the roles of "reference' and "device under test" flipped.)
Frequency Drift
After about 16 days, the frequency plot shows a gradual drift in the maser's frequency. The trend over the five days is a drift of about 1x10-13 per day.
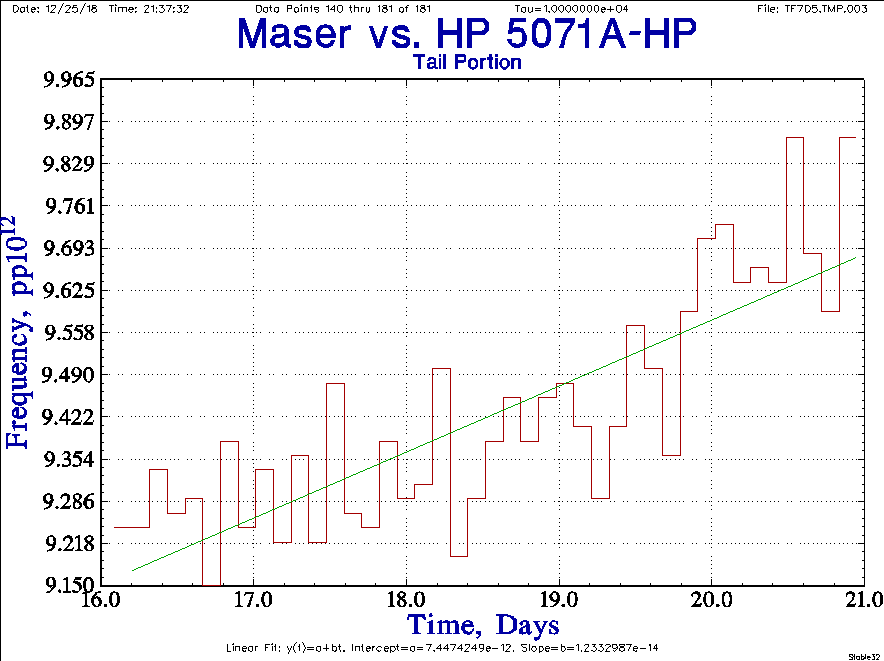
I am cautious about this interpretation, though. If you look at the full data run in just the right way, you can see a sinusoidal pattern and this segment could be part of that, though it seems to be of greater magnitude.
However, using Stable32 to remove the frequency offset from the center section of the data shows that there is essentially no frequency drift during that period: